Grafo de Desargues

Grafo de Desargues
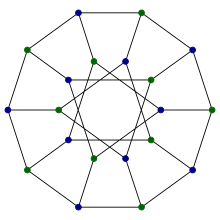O grafo de Desargues
Nomeado em honra a	Girard Desargues
vértices	20
arestas	30
Raio	5
Diâmetro	5
Cintura	6
Automorfismos	240 (S5× Z/2Z)
Número cromático	2
Índice cromático	3
Propriedades	Cúbico Hamiltoniano simétrico distância-regular Bipartido

No campo da matemática da teoria dos grafos o grafo de Desargues é um grafo cúbico, distância-transitivo com 20 vértices e 30 arestas. É nomeado em honra a Girard Desargues, surge a partir de diferentes construções combinatória, tem um elevado nível de simetria, é o único conhecido cubo parcial cúbico não-planar , e tem sido aplicado em bases de dados químicos.

O nome "grafo de Desargues" também tem sido usado para se referir ao complemento do grafo de Petersen.

Construções

Existem várias maneiras diferentes de construir o grafo de Desargues:

• É o grafo de Petersen generalizado G(10, 3). Para formar o grafo de Desargues desta forma, conecte dez dos vértices em um decágono regular, e conecte os outros dez vértices em uma estrela de dez pontas que conecta os pares de vértices a uma distância três em um segundo decágono. O grafo de Desargue consiste das 20 arestas destes dois polígonos juntamente com 10 arestas adicionais de pontos de conexão de um decágono para os pontos correspondentes do outro.
• É o grafo de Levi da configuração de Desargues. Esta configuração é composta por dez pontos e dez linhas descrevendo dois triângulos em perspectiva, seu centro de perspectiva, e seu eixo de perspectiva. O grafo de Desargues tem um vértice para cada ponto, um vértice para cada linha, e uma aresta para cada par de linhas de ponto incidente. O teorema de Desargues, nomeado em honra ao matemático francês do século 17 Girard Desargues, descreve um conjunto de pontos e linhas que formam essa configuração, e a configuração e o grafo devem seu nome a ela.
• É a cobertura bipartida dupla do grafo de Petersen, formada pela substituição de cada vértice do grafo de Petersen por um par de vértices e cada aresta do grafo de Petersen por um par de arestas cruzadas.
• É o grafo de Kneser bipartido H_5,2. Seus vértices podem ser rotulados pelos dez subconjuntos de dois elementos e os dez subconjuntos de três elementos de um conjunto de cinco elementos, com uma aresta conectando dois vértices quando um dos conjuntos correspondentes é um subconjunto do outro.
• O grafo de Desargues é Hamiltoniano e pode ser construído pela notação LCF: [5,−5,9,−9]⁵

Propriedades algébricas

O grafo de Desargues é um grafo simétrico: tem simetrias que levam qualquer vértice para qualquer outro vértice e qualquer aresta para qualquer outra aresta. Seu grupo de simetria tem ordem 240, e é isomórfico ao o produto de um grupo simétrico em 5 pontos, com um grupo de ordem 2.

Pode-se interpretar esta representação de produtos do grupo de simetria em termos de construções do grafo de Desargues: o grupo simétrico em cinco pontos é o grupo de simetria da configuração de Desargues, e o subgrupo de ordem-2 troca os papéis dos vértices que representam pontos da configuração de Desargues e os vértices que representam as linhas. Como alternativa, em termos do grafo bipartido de Kneser, o grupo simétrico em cinco pontos de age em separado sobre os subconjuntos de cinco pontos de dois elementos e de três elementos, e a complementação dos subconjuntos formam um grupo de ordem dois que transforma um tipo de subconjunto em outro. O grupo simétrico em cinco pontos é também o grupo de simetria do grafo de Petersen, e o subgrupo de ordem-2 troca os vértices dentro de cada par de vértices formados na construção da dupla cobertura.

O grafo de Petersen generalizado G(n, k) é vértice-transitivo se e somente se n = 10 e k = 2 ou se k² ≡ ±1 (mod n) e é aresta-transitivo somente nos seguintes sete casos: (n, k) = (4, 1), (5, 2), (8, 3), (10, 2), (10, 3), (12, 5), (24, 5). Assim, o grafo de Desargues é um dos apenas sete grafos de Petersen generalizados simétricos. Entre estes sete grafos estão o grafo cúbico G(4, 1), o grafo de Petersen G(5, 2), o grafo de Möbius–Kantor G(8, 3), o grafo dodecaédrico G(10, 2) e o grafo de Nauru G(12, 5).

O polinômio característico do grafo de Desargues é:

$(x-3)(x-2)^{4}(x-1)^{5}(x+1)^{5}(x+2)^{4}(x+3).\,$

Portanto o grafo de Desargues é um grafo integral: seu espectro consiste inteiramente de inteiros.

Aplicações

Em química, o grafo de Desargues é conhecido como o grafo de Desargues-Levi; é utilizado para organizar sistemas de estereoisômeros de compostos 5-ligantes. Nesta aplicação, as trinta arestas do grafo correspondem a pseudorotações dos ligantes.

Outras propriedades

O grafo de Desargues tem um número de cruzamento retilíneo 6, e é o menor grafo cúbico com este número de cruzamento (sequência A110507 na OEIS). É o único conhecido cúbico não planar cubo parcial .

O grafo de Desargues tem um número cromático 2, índice cromático 3, raio 5, diâmetro 5 e cintura 6. É também um grafo hamiltoniano, 3-vértice-conectado, e 3-aresta-conectado.

Todos os grafos distância-regular cúbicos são conhecidos. O grafo de Desargues é um destes 13 grafos.

Galeria

• 
  O grafo de Desargues colorido para sobresaltar vários ciclos.
• 
  O índice cromático do grafo de Desargues é 3.
• 
  O número cromático do grafo de Desargues é 2.